b树
b树就是平衡M叉树。跟平衡二叉树类似,avl的非叶子节点只有一个关键字,b树的非叶子节点有M-1个关键字。M-1个关键字将数据划分为M段,每个儿子节点对应一段。b树的叶子结点和非叶子节点都存放数据。
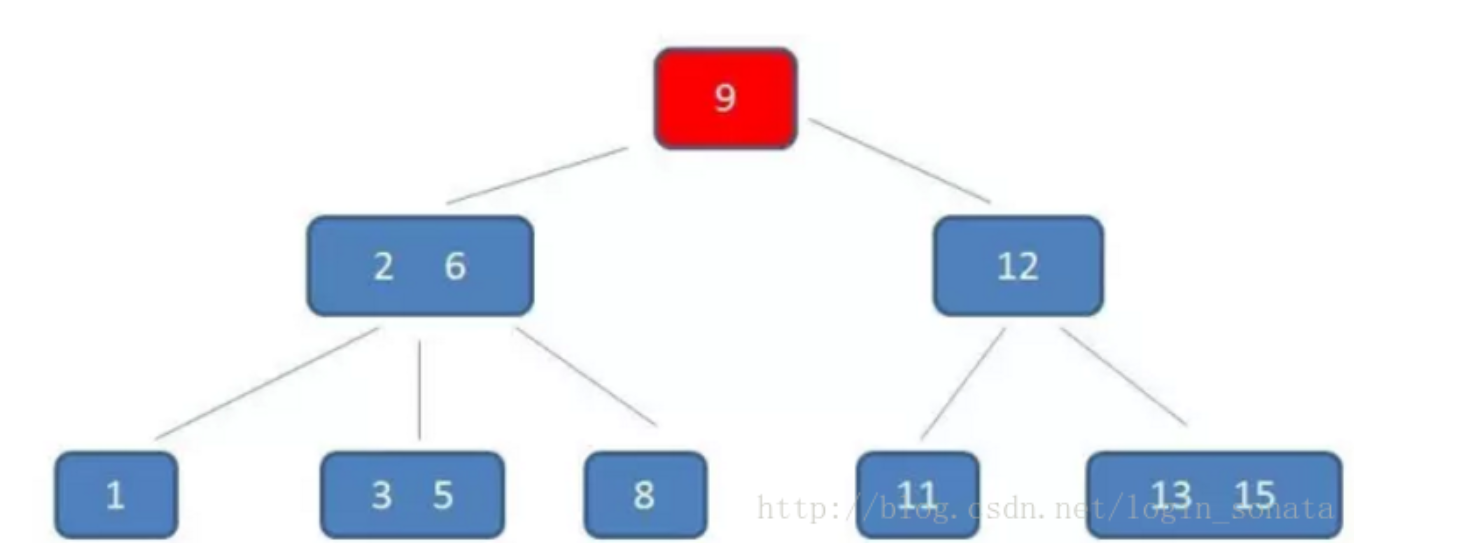
一个M阶的b树具有如下几个特征:
- 定义任意非叶子结点最多只有M个儿子,且M>2;
- 根结点的儿子数为[2, M];
- 除根结点以外的非叶子结点的儿子数为[M/2, M],向上取整;
- 非叶子结点的关键字个数=儿子数-1;
- 所有叶子结点位于同一层;
- k个关键字把节点拆成k+1段,分别指向k+1个儿子,同时满足查找树的大小关系。
有关b树的一些特性,注意与后面的b+树区分:
- 关键字集合分布在整颗树中;
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束;
- 其搜索性能等价于在关键字全集内做一次二分查找;
b+树
b+树是b树的变体,区别是b+树非叶子节点有M个关键字,并且不在非叶子结点存储数据,同时b+树的叶子结点之间也有指针相连。
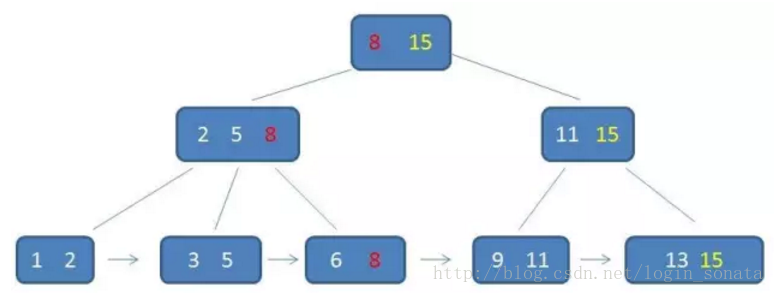
M阶的b+树的特征:
- 有M棵子树的非叶子结点中含有M个关键字(b树是M-1个),这些关键字不保存数据,只用来索引,所有数据都保存在叶子节点(b树是每个关键字都保存数据)。
- 所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的非叶子结点可以看成是索引部分,结点中仅含其子树中的最大(或最小)关键字。
- 通常在b+树上有两个头指针,一个指向根结点,一个指向关键字最小的叶子结点。
- 同一个数字会在不同节点中重复出现,根节点的最大元素就是b+树的最大元素。
b+树相比于b树的查询优势:
- b+树的中间节点不保存数据,所以磁盘页能容纳更多节点元素,更“矮胖”;
- b+树查询必须查找到叶子节点,b树只要匹配到即可不用管元素位置,因此b+树查找更稳定(并不慢);
- 对于范围查找来说,b+树只需遍历叶子节点链表即可,b树却需要重复地中序遍历;