希尔排序

排序原理

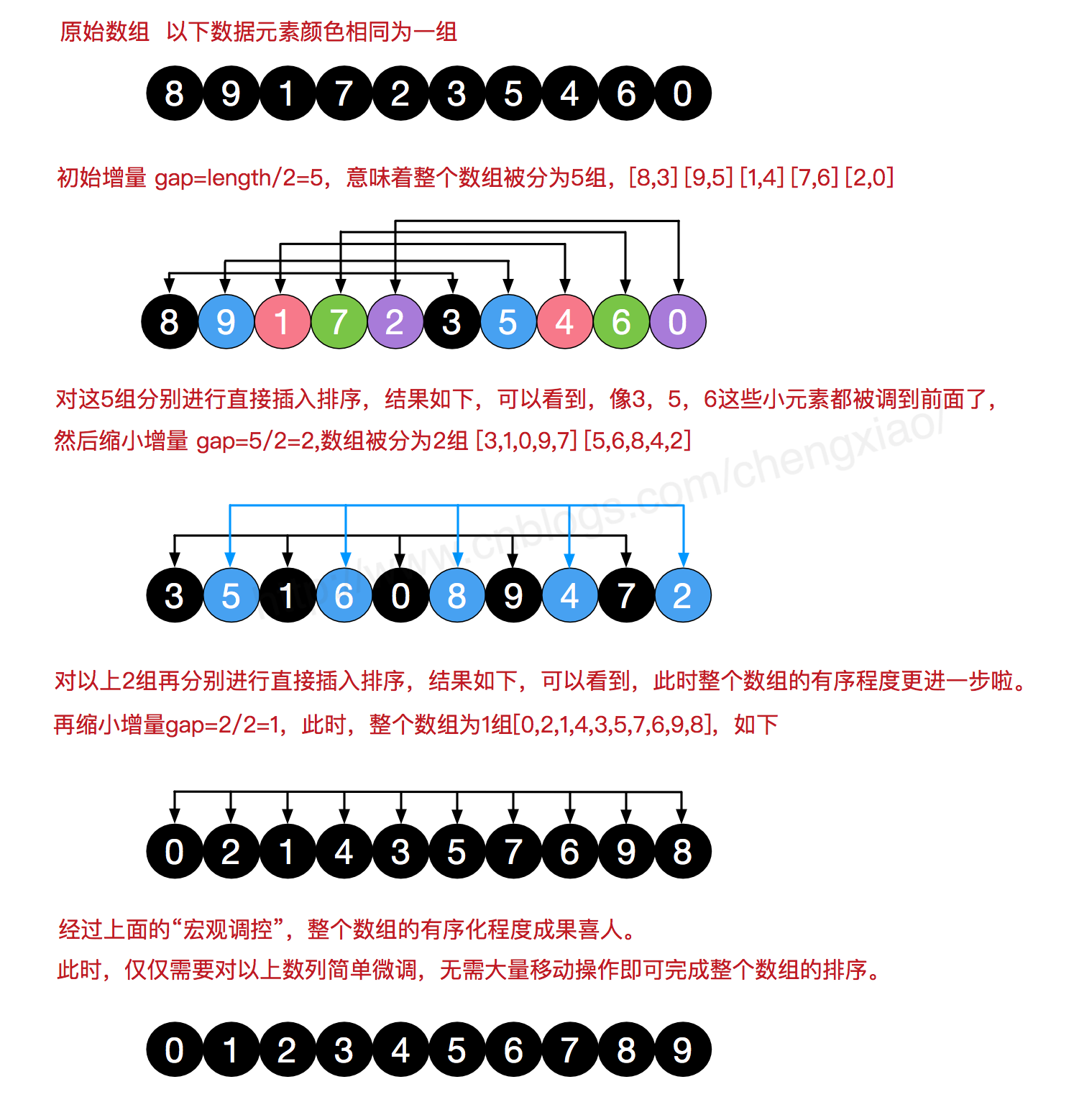
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

简单插入排序很循规蹈矩，不管数组分布是怎么样的，依然一步一步的对元素进行比较，移动，插入，比如[5,4,3,2,1,0]这种倒序序列，数组末端的0要回到首位置很是费劲，比较和移动元素均需n-1次。

而希尔排序在数组中采用跳跃式分组的策略，通过某个增量将数组元素划分为若干组，然后分组进行插入排序，随后逐步缩小增量，继续按组进行插入排序操作，直至增量为1。希尔排序通过这种策略使得整个数组在初始阶段达到从宏观上看基本有序，小的基本在前，大的基本在后。然后缩小增量，到增量为1时，其实多数情况下只需微调即可，不会涉及过多的数据移动。

好像有人证明希尔排序的时间复杂度是O(n^1.3)

动图：

核心

希尔排序的核心就是通过步长比较大的那几次插入排序保证了数组是基本有序的，然后再进行步长小的插入排序时不需要进行过多的比较和交换。

在进行每一轮插入排序时，遇到第一个非逆序时就直接break就行了，我认为这才是希尔排序比简单插入排序快的原因。而网上大量博客都没说清楚，甚至代码里都没有这个break，这样性能可能还没有普通插入排序高。

代码

vector<int> sortArray(vector<int>& nums) {
    int n = nums.size();
    for(int d=n/2;d>=1;d/=2){ // 步长d，共分为d组
        for(int i=d;i<n;i++){  // 对每个元素进行组内插入排序
            for(int j=i;j>=d;j-=d){ // 组内插入排序
                if(nums[j-d]>nums[j]) swap(nums[j-d], nums[j]);
                else break; // 希尔排序的核心就是这个break，遇到非逆序时就break
            }
        }
    }
    return nums;
}