Jepson's Blog
0%

Posted on

题目

当 k 个日程安排有一些时间上的交叉时（例如 k 个日程安排都在同一时间内），就会产生 k 次预订。

给你一些日程安排 [start, end) ，请你在每个日程安排添加后，返回一个整数 k ，表示所有先前日程安排会产生的最大 k 次预订。

思路

插旗法：进入一个区间的时候将该点坐标对应的值+1，代表插上一面进入的🚩，离开时将该点坐标值-1，代表插上一面离开的🚩，在同一个点可以同时插进入的旗或离开的旗，因为这样并不形成区间重叠。

通过计数器cnt可以得到当前重叠次数，如果不能重叠则cnt>1就返回false（如我的日程安排表一），如果不能重叠三次就cnt>2再返回false（如我的日程安排表二），如果要求最大重叠次数就返回cnt最大值（如我的日程安排表三）。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
map<int, int> rec;
int book(int start, int end) {
    rec[start] ++;
    rec[end] --;
    int ans = 0;
    int cnt = 0;
    for(auto &a: rec){
        /*
        if(cnt>1){
            rec[start] --;
            rec[end] ++;
            return false;
        }
        */
        cnt += a.second;
        ans = max(ans, cnt);
    }
    return ans;
}

Posted on Edited on

桶排序

桶排序是一种用空间换取时间的排序，桶排序重要的是它的思想，而不是具体实现，时间复杂度最好可能是线性O(n)，桶排序不是基于比较的排序而是一种分配式的。

桶排序的思想为：将待排序的序列分到若干个桶中，每个桶内的元素再进行个别排序。 当然桶排序选择的方案跟具体的数据有关系，桶排序是一个比较广泛的概念，并且计数排序是一种特殊的桶排序，基数排序也是建立在桶排序的基础上。在数据分布均匀且每个桶元素趋近一个时间复杂度能达到O(n),但是如果数据范围较大且相对集中就不太适合使用桶排序。

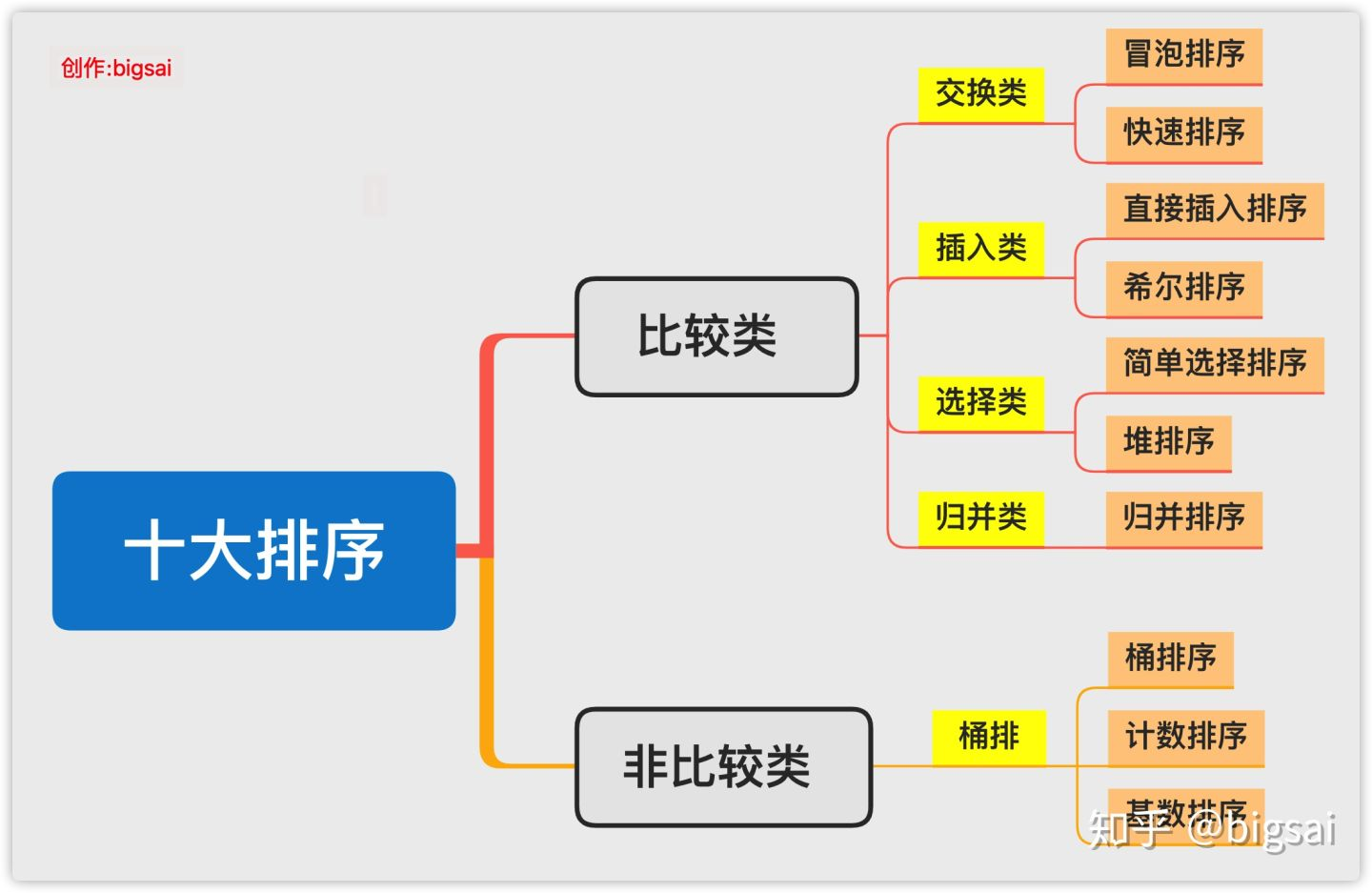
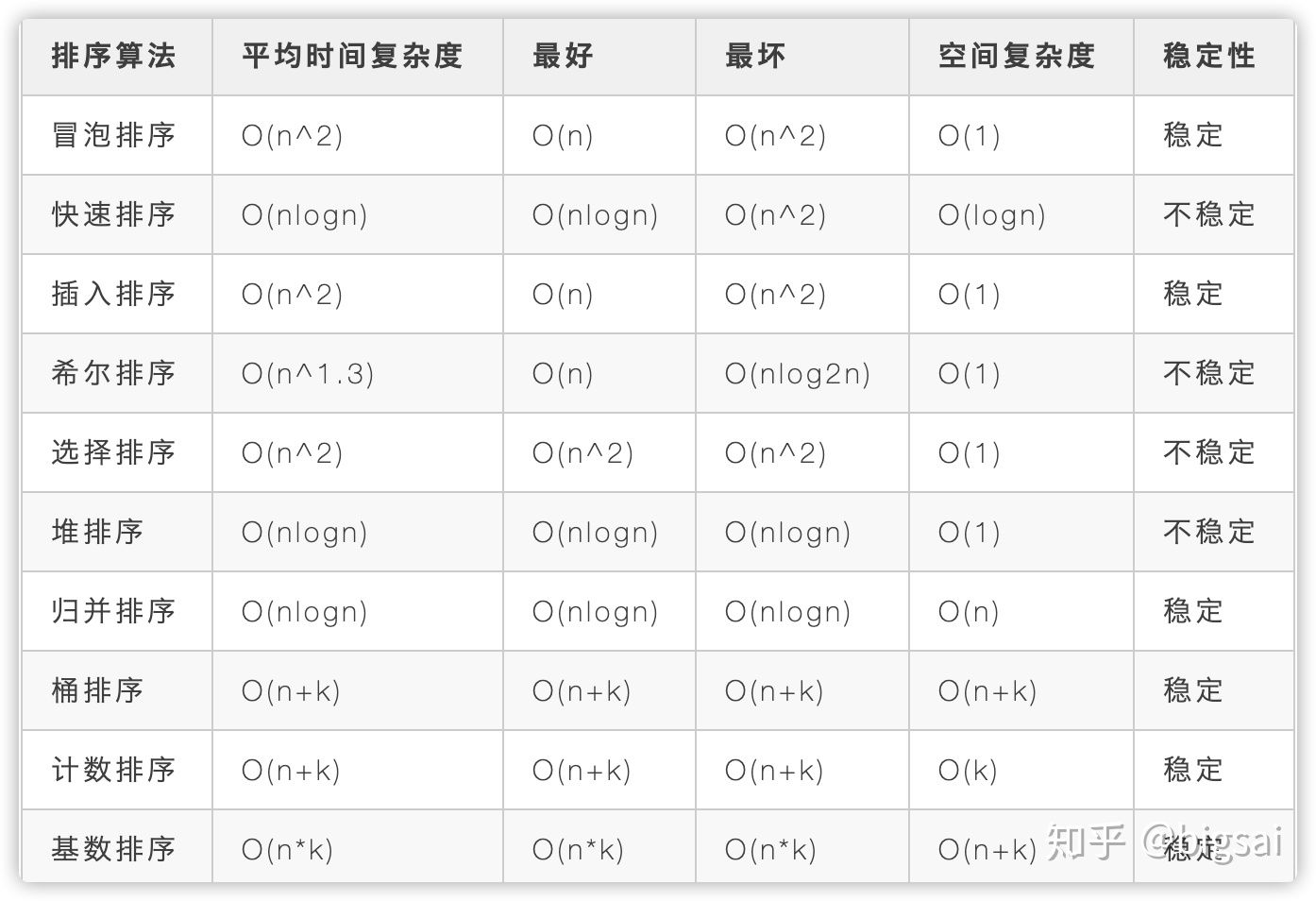
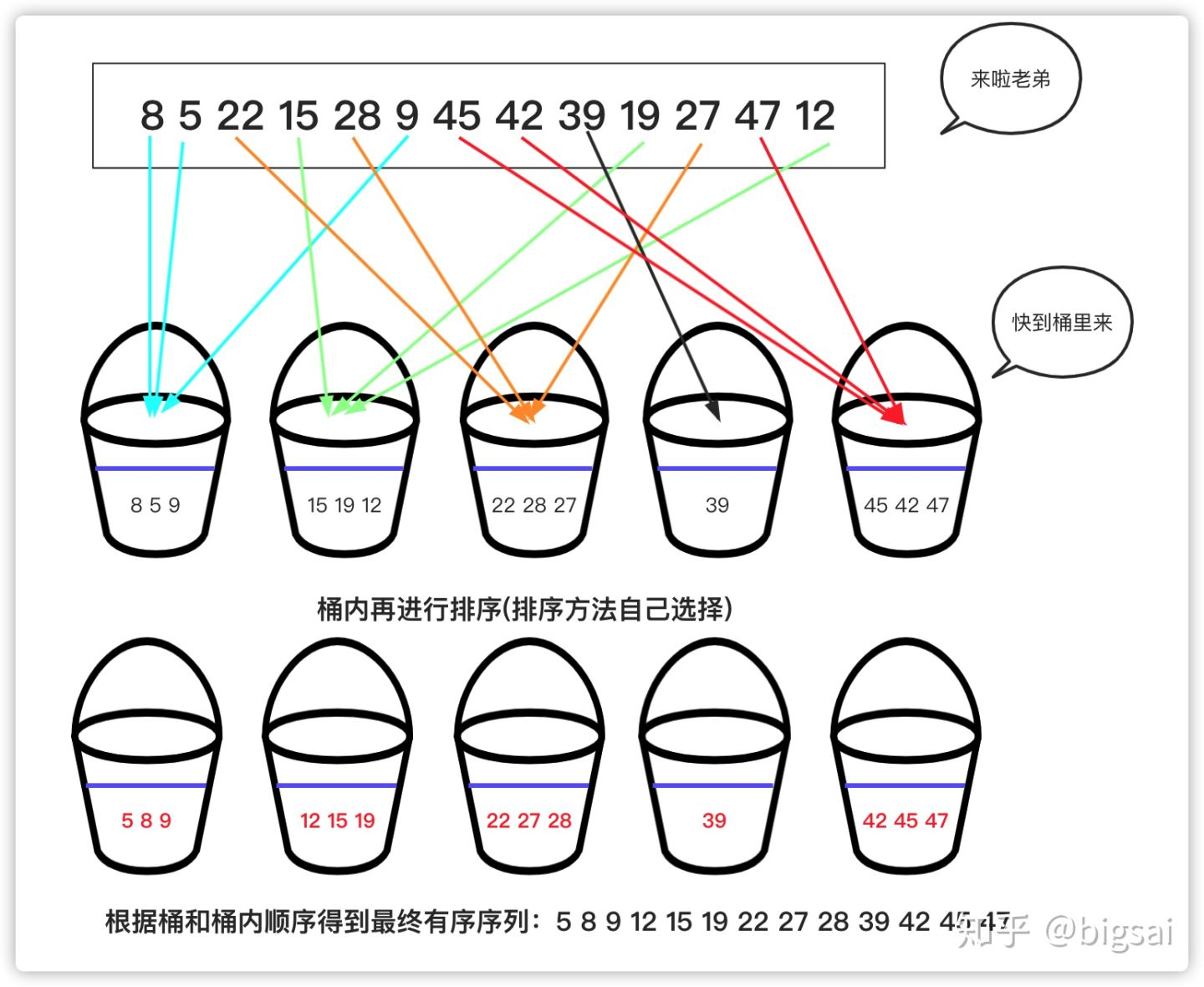
20220224104715

计数排序

计数排序是一种特殊的桶排序，每个桶的大小为1，每个桶不在用List表示，而通常用一个值用来计数。

在设计具体算法的时候，先找到最小值min，再找最大值max。然后创建这个区间大小的数组，从min的位置开始计数，这样就可以最大程度的压缩空间，提高空间的使用效率。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static void countSort(int a[])
{
  int min=Integer.MAX_VALUE;int max=Integer.MIN_VALUE;
  for(int i=0;i<a.length;i++)//找到max和min
  {
    if(a[i]<min) 
      min=a[i];
    if(a[i]>max)
      max=a[i];
  }
  int count[]=new int[max-min+1];//对元素进行计数
  for(int i=0;i<a.length;i++)
  {
    count[a[i]-min]++;
  }
  //排序取值
  int index=0;
  for(int i=0;i<count.length;i++)
  {
    while (count[i]-->0) {
      a[index++]=i+min;//有min才是真正值
    }
  }
}

基数排序

基数排序也称为卡片排序，基数排序的原理就是多次利用计数排序(计数排序是一种特殊的桶排序)，但是和前面的普通桶排序和计数排序有所区别的是，基数排序并不是将一个整体分配到一个桶中，而是将自身拆分成一个个组成的元素，每个元素分别顺序分配放入桶中、顺序收集，当从前往后或者从后往前每个位置都进行过这样顺序的分配、收集后，就获得了一个有序的数列。

核心

基数排序就是进行d论计数排序，d是最大数字的长度。每一轮排序就是针对每个数字的某一位做计数排序，每一轮排序的结果是所有元素不一定有序，但是在这一位上是有序。然后在对下一位进行下一轮的计数排序，所有数字在该位上是有序的，该位相等的那些数字在上一位是有序的。所以一共进行d论计数排序之后，所有数字都是有序的。

代码

https://jepson-song.github.io/2021/12/01/%E5%9F%BA%E6%95%B0%E6%8E%92%E5%BA%8F/

Posted on

排序原理

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

简单插入排序很循规蹈矩，不管数组分布是怎么样的，依然一步一步的对元素进行比较，移动，插入，比如[5,4,3,2,1,0]这种倒序序列，数组末端的0要回到首位置很是费劲，比较和移动元素均需n-1次。

而希尔排序在数组中采用跳跃式分组的策略，通过某个增量将数组元素划分为若干组，然后分组进行插入排序，随后逐步缩小增量，继续按组进行插入排序操作，直至增量为1。希尔排序通过这种策略使得整个数组在初始阶段达到从宏观上看基本有序，小的基本在前，大的基本在后。然后缩小增量，到增量为1时，其实多数情况下只需微调即可，不会涉及过多的数据移动。

好像有人证明希尔排序的时间复杂度是O(n^1.3)

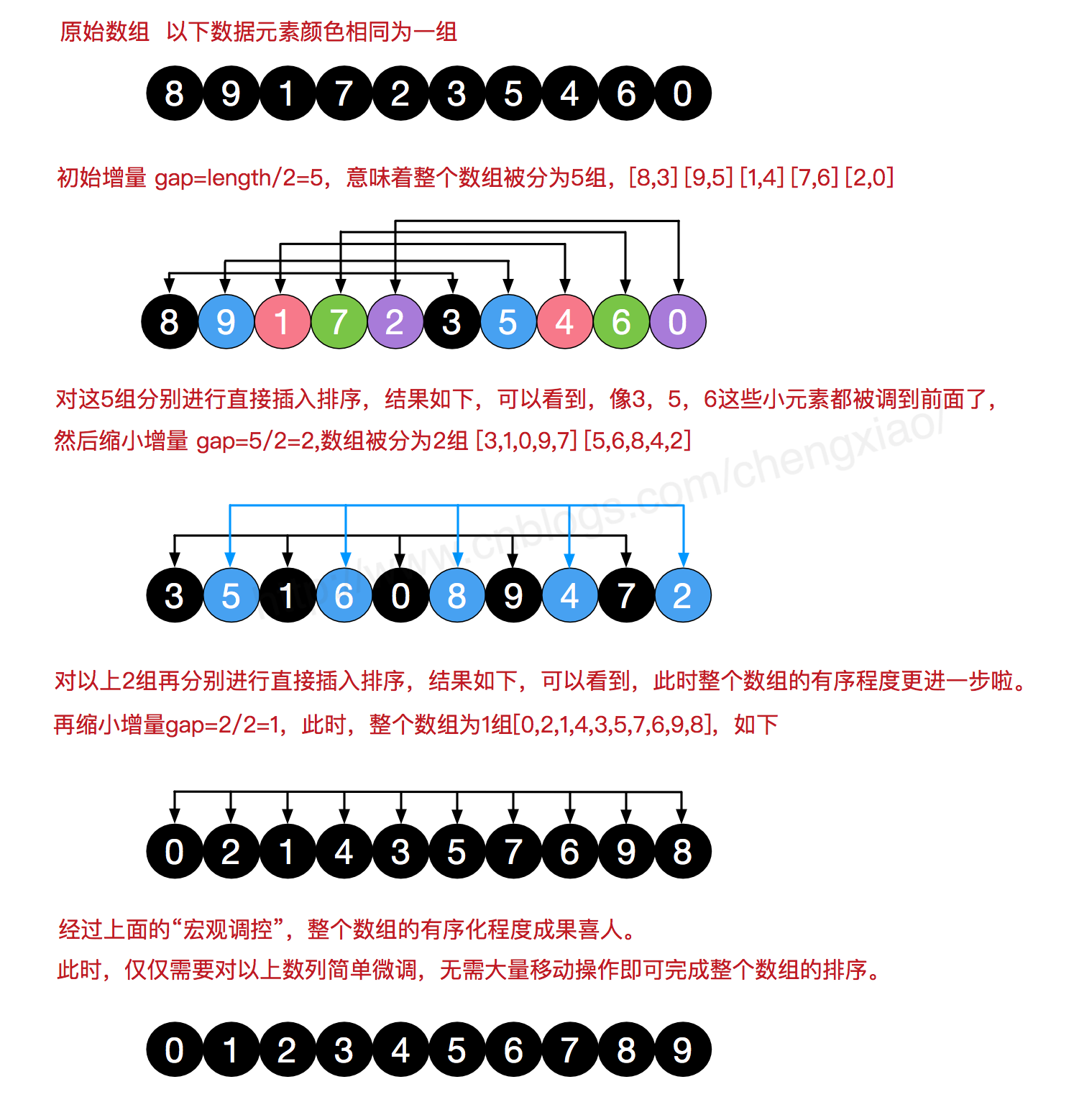
20220224103652

动图：

20220224103635

核心

希尔排序的核心就是通过步长比较大的那几次插入排序保证了数组是基本有序的，然后再进行步长小的插入排序时不需要进行过多的比较和交换。

在进行每一轮插入排序时，遇到第一个非逆序时就直接break就行了，我认为这才是希尔排序比简单插入排序快的原因。而网上大量博客都没说清楚，甚至代码里都没有这个break，这样性能可能还没有普通插入排序高。

代码

1
2
3
4
5
6
7
8
9
10
11
12
vector<int> sortArray(vector<int>& nums) {
    int n = nums.size();
    for(int d=n/2;d>=1;d/=2){ // 步长d，共分为d组
        for(int i=d;i<n;i++){  // 对每个元素进行组内插入排序
            for(int j=i;j>=d;j-=d){ // 组内插入排序
                if(nums[j-d]>nums[j]) swap(nums[j-d], nums[j]);
                else break; // 希尔排序的核心就是这个break，遇到非逆序时就break
            }
        }
    }
    return nums;
}

Posted on

描述

给定一个长度为 n 的数组 arr，求它的最长严格上升子序列的长度。
所谓子序列，指一个数组删掉一些数（也可以不删）之后，形成的新数组。例如 [1,5,3,7,3] 数组，其子序列有：[1,3,3]、[7] 等。但 [1,6]、[1,3,5] 则不是它的子序列。

。
数据范围： 0 <= n <= 1000
要求：时间复杂度 O(n^2)，空间复杂度 O(n)

示例1

输入：[6,3,1,5,2,3,7]
返回值：4
说明：该数组最长上升子序列为 [1,2,3,7] ，长度为4

思路

维护一个伪上升子序列，遍历数组中每一个值，二分找到伪上升子序列中第一个比它大的值，然后将其替换掉，如果没有则直接插入到伪上升子序列最后。

代码

  1. 手写二分

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
        int LIS(vector<int>& arr) {
        // write code here
        int ans = 0;
        int n = arr.size();
        int b[n];
        int lb, rb;
        lb = rb = 0;
        int l, r, mid;
        for(int i=0;i<n;i++){
            l = lb;
            r = rb;
            while(l<r){
                mid = (l+r)/2;
                if(b[mid]>arr[i]) r = mid;
                else l = mid+1;
            }
            if(l>=lb&&l<=rb-1) b[l] = arr[i];
            else b[rb++] = arr[i];
        }
        return rb-lb;
    }
    }

  2. upper_bound

    upper_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

    lower_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
        int LIS(vector<int>& a) {
        // write code here
        int n = a.size();
        vector<int> b;
        for(int i=0;i<n;i++){
            int p = upper_bound(b.begin(), b.end(),a[i])-b.begin();
            if(p==b.size()) b.push_back(a[i]);
            else b[p] = a[i];
        }
        return b.size();
    }